D'Arcy-Weisbach Equation

Introduction

This Equation is widely used in calculating friction losses in Pipe Flow of Fluids. It is considered as best empirical relation for pipe-flow resistance.

The Darcy-Weisbach Equation used in conjunction with the Moody Diagram (for obtaining Fanning friction factors) is considered by many people to be the most reliable method for calculating either Frictional Pressure Loss or Frictional Head Loss for the flow of in-compressible fluids in pipes.

Equation

In terms of Frictional Head Loss

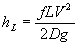
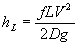
In terms of Frictional Pressure Drop

h  =  head loss

f  =  darcy friction factor  [ f is a complex function of the Reynolds Number and Relative Roughness]

L  =  pipe length

D  =  pipe diameter

V  =  flow velocity

g  =  acceleration of gravity

r  =  fluid density

Features

- It is applicable to any Gas and Liquid

- It is more accurate then Hazen-Williams Equation

- It is Complex then Hazen-Williams Equation

Application

The most important parameter to understand the Darcy Equation is the Darcy Friction Factor (f). It is a Dimensionless quantity. It is also known as Moody Friction Factor and is larger then Fanning Friction Factor by Four Times.  

Darcy Friction Factor is 4 time as large as the Fanning Friction factors

Laminar Flow

For laminar Flow (NRe < 2000) the Darcy friction factor (f) is only function of Reynolds Number and independent of Relative Roughness. and the Formula is reduced to f = 64/NRe. This equation is known as short / simplified form of Hagen-Poiseuille Equation.

Darcy Friction Factor = f =  64/NRe  (for laminar flow having Reynolds Number below 2,000)

Turbulent Flow (4,000 < NRe < 100,000)  but Hydraulically Smooth Pipe (e = 0)

For hydraulically smooth pipes (e = 0) such as glass, copper and plastic tubing in turbulent flow, use Blasius Equation for calculating the Darcy Friction Factor. Sometimes Blasius Equation can be used in rough pipes as well.



"Hydraulically Smooth Pipe means that the roughness on the wall of the pipe is less the thickness of the laminar sub layer of the turbulent flow."

A hydraulically smooth pipe has excellent hydraulic properties that allow fluids to be flow with a minimum head loss.

Turbulent Flow (4,000 < NRe < 100,000)  and Rough Pipe (e ≠ 0)

Moody Diagram is Used for Darcy Friction Factor. Moody Diagram can be said a graphical solution of Colebrook Equation. The factor can be determined by its Reynolds number and the Relative Roughness of the Pipe. The rougher the pipe the more turbulent the flow is through that pipe.  The relative roughness of a pipe is given by

Relative Roughness of Pipe =  ε / D  

where ε = Absolute Roughness 
           D = Hydraulic Diameter

Friction factor depends on the NRe and (if turbulent) on the pipe relative roughness. The relationship between the friction factor, Re, and relative roughness is schematically presented in the following.  This diagram is generally referred to as the Moody Diagram.




Absolute Roughness is usually defined for a material and can be measured experimentally. Roughness Values are normally given in mm. 

For every circular shape there is diameter and for every non-circular there is Hydraulic Diameter. I personally say it equivalent diameter of a non-circular shape. The hydraulic diameter is not the same as the geometrical diameter in a non-circular duct or pipe. Normally we encounter the two types of non-circular shapes for flow calculations; 1) Rectangular Duct 2) Annular Shape

The hydraulic diameter (aka hydraulic mean diameter) is used for a fluid flowing in a pipe, duct or other conduit of any shape. Hydraulic mean diameter provides a method by which non-circular pipe work and ducting may be treated as circular for the purpose of pressure drop and fluid flow rate calculations. This uses the perimeter and the area of the conduit to provide the diameter of a pipe which has proportions such that conservation of momentum is maintained.

It works well for turbulent flow where geometry is less important, but should not be used for the laminar flow regime, which is influenced to a much higher degree by conduit geometry.

The hydraulic diameter is calculated as 4 times the flow area divided by the wetted perimeter of the conduit. The hydraulic diameter concept applies for rectangular ducts width to height ratio is less than 4 (which is the usual case.

D(h) = 4  x  Area / Wetted Perimeter

where;

D(h) = Hydraulic Diameter
Area = Cross Sectional Area of the Duct
P = Wetted Perimeter of the Duct (Total Length of the surface which is in contact with the fluid in one cross section)


Colebrook-White Equation

For Reynold's Number Greater then 4,000 (Turbulent Flow) the Colebrook Equation is