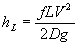Redlich-Kwong Equation of State

In physics and thermodynamics, the Redlich–Kwong equation of state is an empirical, algebraic equation that relates temperature, pressure, and volume of gases. It is generally more accurate than the van der Waals equation and the ideal gas equation at temperatures above the critical temperature. It was formulated by Otto Redlich and Joseph Neng Shun Kwong in 1949.

Hagen-Poiseuille equation

Hagen-Poiseuille's Equation can be used to determine the pressure drop of a constant viscosity Newtonian fluid exhibiting laminar flow through a rigid pipe. Non-newtonian liquids do not obey Poiseuille's law because their viscosities are velocity dependent. The assumption of
streamlined (laminar) flow is built in to Poiseuille's law. If turbulence occurs than you must be very careful about using Poiseuille's law to calculate flow rates. If turbulence does occur in the flow then the volume flow rate is dramatically reduced.

Viscosity

Viscosity is the resistance of a fluid to flow. Virtually all fluids have viscosity which generally changes as a function of temperature; although different types of fluids exhibit different types of fluid–shear velocity dependencies.

“When a fluid or semisolid is subjected to a constant shearing force it flows, i.e., it deforms continuously at a velocity that increases as the applied shearing force increases.” Viscosity quantifies the resistance of the fluid to flow

Introduction

Viscosity is a quantitative measure of fluid’s resistance to flow (shear stress) at a given temperature. This resistance arises from the attractive forces between the molecules of the fluid. A fluid will only flow if enough energy is supplied to overcome these forces.

Dynamic Viscosity / Viscosity

The dynamic viscosity (η) of a fluid is a quantitative measure of the resistance it offers to relative shearing motion.
Dynamic viscosity, which is also referred to as absolute viscosity, or just viscosity, is the quantitative expression of a fluid’s resistance to flow (shear). Fluid dynamicists, chemical engineers and mechanical engineers commonly consider the use of the Greek letter mu (µ) as the symbol to denote dynamic viscosity.

Units

The SI unit is pascal-second [Pa.s] or millipascal-second [mPa.s]:

    1 Pa.s = 1000 mPa.s
    The SI unit is named after Blaise Pascal.

Other commonly used units are poise [P] or centipoise [cP]:

    1 P = 100 cP
    This unit is named after Jean Poiseuille

    1 cP = 1 mPa.s = 0.001 Pa.s = 0.01 P

However, the most common expression is centipoise (cP), which is mainly used in ASTM standards.

Kinematic Viscosity

It is defined as the ratio of absolute viscosity to the density of fluid. Kinematic viscosity describes a substance's flow behavior under the influence of Earth's gravity. It is dynamic viscosity divided by density ρ, rho, which is defined as mass per volume. The quantity mass carries the gravitational influence. Kinematic viscosity is sometimes called the diffusivity of momentum.

        ν= η/ρ

Units

The SI unit is square-meters per second  [m2/s] or square-millimeters per second [mm2/s]:

    1 m2/s = 1 000 000 mm2/s

Other commonly used units are stokes [St] or centistokes [cSt]:

    1 St = 100 cSt

This unit is named after George G. Stokes.

    1 cSt = 1 mm2/s

 It should be noted that water (H2O) at 20 degrees centigrade is about 1 cSt.

Relation of Kinematic Viscosity with Dynamic Viscosity

Limitations

The above equation holds only when

1-Fluid is Newtonian

2-Specific Gravity Remains the Same

Application

Liquids are generally considered viscous if viscosity is more then 40 centipoise (cp). Centrifugal pumps are not recommended for fluid having viscosity more then 300 centipoise (cp).

The viscosity of liquids decreases with increase the  temperature. Typically 2% per degree C. For some materials (fruit juices) the Temperature effect follows an Arrhenius relationship. 

Viscosity of gases increases with the increase the temperature.

Hazen-Williams Equation

Introduction

The Hazen-Williams equation is an empirical formula used to model the friction head loss of water flowing through pipe. The accuracy of the Hazen-Williams is less than that of the C.F. Colebrook equation. This equation uses the coefficient C to specify the pipes roughness, which is not based on a function of the Reynolds number, as in other pressure loss equations. 

It is also possible to use Hazen-Williams to model fluids other than water as long as the viscosity is approximately 1.130 centistokes.

Calculating Head Loss

Where:

C      = Friction Factor (Hazan William Constant)

d       = Inside diameter of pipes (in)

Q       = Flow rate in Gallons per minute of water

L      = Length of pipe (ft)

hf     = Friction head loss (ft)

Limitations

1. it should only be used for water between the temperature of 55 degrees Fahrenheit (12.8 deg C) and 65 degrees Fahrenheit (18.3 deg C). The formula is popular with civil engineers who constantly need to make calculations for water flow through pipe in the ambient atmosphere.

2. Hazen William Equation can only be used in equation can only be used when water is flowing within the 'turbulent' flow range

Applications

The Hazen William formula has now become adopted through the world as the pressure loss formula to use for the hydraulic design of fire sprinkler systems and in almost all cases the use of the hazen william formula will provide adequate answers. The Hazen William formula can also be used for the calculation of water mist systems where the system pressure does not exceed 12 bar (low pressure water mist systems) or the water velocity does not exceed 7.6 m/s and the minimum pipe size is 20 mm in the case of intermediate and high pressure water mist systems.

Ideal Gas Equation

Introduction

The three historically important gas laws derived relationships between two physical properties of a gas, while keeping other properties constant:




It is the most basic equation of state, assuming that the particles in the gas behave in such a way that they do not interact with each other at all, and approximate point masses. This makes the math very simple as the extensive state of an ideal gas is only a function of temperature, pressure, and volume.

P V = n R T

Application

There are three common applications of Ideal Gas Equation.

• Calculation of Molar Volume 

• Calculation of Density 

• Calculation of Molar Mass (weight of one mole) 

Properties of the gaseous state predicted by the ideal gas law are within 5% for gases under ordinary conditions.

Peng-Robinson Equation of State

Introduction

The Peng-Robinson EOS has become the most popular equation of state for natural gas systems in the petroleum industry.



In the form of Pressure



Where 

 

Reynolds Number

Introduction

The Reynolds Number expresses the ratio of inertial (resistant to change or motion) forces to viscous (heavy and gluey) forces and consequently quantifies the relative importance of these two types of forces for given flow conditions. The Reynolds number is a dimensionless number. High values of the parameter (on the order of 10 million) indicate that viscous forces are small and the flow is essentially inviscid.

 

For Pipes

 = Hydraulic Diameter (m)

 = Volumetric flow rate (m3/s)

 = Pipe cross-sectional area (m²)

 = Mean Velocity of the Fluid (m/s)

 = Dynamic Viscosity of the fluid (Pa·s = N·s/m² = kg/(m·s)).

 = Kinematic Viscosity of the fluid  ( (m²/s). 

Explanation

At relatively low values of the Reynolds number, the viscous force is relatively more important, and disturbances in the flow are damped out by viscosity.  Thus, it is difficult for disturbances to grow and sustain themselves. On the other hand, at relatively large values of the Reynolds number, the damping of disturbances by viscosity is less effective, and inertia is more important, so that disturbances can perpetuate themselves.  This is the basic reason why the Reynolds number serves as a measure for determining whether the flow is laminar or turbulent.

Application

They are used to characterize different flow regimes within a similar fluid, such as laminar or turbulent flow:

laminar when Re < 2300

transient when 2300 < Re < 4000

turbulent when Re > 4000

Laminar flow occurs at low Reynolds numbers, where viscous forces are dominant, and is characterized by smooth, constant fluid motion, while Turbulent Flow occurs at high Reynolds numbers and is dominated by inertial forces, which tend to produce random eddies, vortices and other flow fluctuations.

Turbulent flow is a flow regime in which the movement of the fluid particles is chaotic, eddying, and unsteady.

 Due to the complex nature of turbulent flows, scientists and engineers use empirical rather than theoretical approaches to model and design processes and machinery involving fluids.

Colebrook-White Equation

Introduction

The Colebrook equation has long been used for calculating the friction factor, f, for in-compressible and some compressible flows in uniform pipes, ducts, and conduits. It is asymptotic to both the accepted smooth-surface and rough-surface pipe equations.

Although widely used, the Colebrook equation is iterative because the unknown friction factor appears on both sides of the equation. To solve for this unknown, one must start by somehow estimating the f value on the right side of the equation, solve for the new f on the left, enter the new value back on the right side, and continue this process until there is a balance on both sides of the equation within an arbitrary difference. (An exact solution to this equation has remained elusive, to date.)

This difference must be small yet accommodate all ε/D (surface roughness/hydraulic diameter) and Re (Reynolds number) values without causing endless computations. The method is labor intensive and complicated even for computers. Add to this the repetitive calculations needed at numerous points in complex flow systems and the task becomes time consuming, to say the least.

For these reasons, many different diagrams have been constructed to simplify the process. A well-known one is the Moody Friction Factor graph. However, reading the chart and interpolating values often leads to inaccuracies. And it would take numerous equations to capture the graphs in software.

A new equation, based on Colebrook’s, has been developed that calculates friction factors in one step.

For ε/D > 0:

This is the Colebrook equation rewritten using a modified Newton iteration for approximating the solution. The modification involves a new factor, A. For ε/D > 0, A is a modified Colebrook equation and calculates the first estimate for the unknown f, or, in this case, 1/f0.5.

Values for f calculated with this equation are based on 69 randomly chosen numbers for Re from 4,000 to 108 and ε/D from 0 (smooth) to 0.05 (rough). They were compared in terms of percent difference from f values calculated with the Colebrook equation after three iterations for each of the same Re and ε/D values (four iterations yielded negligible changes).

For ε/D > 0, all resulting differences are <0.001%. The average difference for all 69 calculations is 0.000134%, with the maximum being 0.000941% and the minimum 0%.

For ε/D = 0, A is derived using leastsquares fit and fine-tuned using trial and error. Only 52 of the 69 numbers were used because of the shorter range of Re (4,000 to 107). All resulting differences are again <0.001%. The average difference for all 52 calculations is 0.000229% with a maximum 0.000519%.

A single equation for A was also developed for all cases:

D'Arcy-Weisbach Equation

Introduction

This Equation is widely used in calculating friction losses in Pipe Flow of Fluids. It is considered as best empirical relation for pipe-flow resistance.

The Darcy-Weisbach Equation used in conjunction with the Moody Diagram (for obtaining Fanning friction factors) is considered by many people to be the most reliable method for calculating either Frictional Pressure Loss or Frictional Head Loss for the flow of in-compressible fluids in pipes.

Equation

In terms of Frictional Head Loss

In terms of Frictional Pressure Drop

h  =  head loss

f  =  darcy friction factor  [ f is a complex function of the Reynolds Number and Relative Roughness]

L  =  pipe length

D  =  pipe diameter

V  =  flow velocity

g  =  acceleration of gravity

r  =  fluid density

Features

- It is applicable to any Gas and Liquid

- It is more accurate then Hazen-Williams Equation

- It is Complex then Hazen-Williams Equation

Application

The most important parameter to understand the Darcy Equation is the Darcy Friction Factor (f). It is a Dimensionless quantity. It is also known as Moody Friction Factor and is larger then Fanning Friction Factor by Four Times.  

Darcy Friction Factor is 4 time as large as the Fanning Friction factors

Laminar Flow

For laminar Flow (NRe < 2000) the Darcy friction factor (f) is only function of Reynolds Number and independent of Relative Roughness. and the Formula is reduced to f = 64/NRe. This equation is known as short / simplified form of Hagen-Poiseuille Equation.

Darcy Friction Factor = f =  64/NRe  (for laminar flow having Reynolds Number below 2,000)

Turbulent Flow (4,000 < NRe < 100,000)  but Hydraulically Smooth Pipe (e = 0)

For hydraulically smooth pipes (e = 0) such as glass, copper and plastic tubing in turbulent flow, use Blasius Equation for calculating the Darcy Friction Factor. Sometimes Blasius Equation can be used in rough pipes as well.



"Hydraulically Smooth Pipe means that the roughness on the wall of the pipe is less the thickness of the laminar sub layer of the turbulent flow."

A hydraulically smooth pipe has excellent hydraulic properties that allow fluids to be flow with a minimum head loss.

Turbulent Flow (4,000 < NRe < 100,000)  and Rough Pipe (e ≠ 0)

Moody Diagram is Used for Darcy Friction Factor. Moody Diagram can be said a graphical solution of Colebrook Equation. The factor can be determined by its Reynolds number and the Relative Roughness of the Pipe. The rougher the pipe the more turbulent the flow is through that pipe.  The relative roughness of a pipe is given by

Relative Roughness of Pipe =  ε / D  

where ε = Absolute Roughness 
           D = Hydraulic Diameter

Friction factor depends on the NRe and (if turbulent) on the pipe relative roughness. The relationship between the friction factor, Re, and relative roughness is schematically presented in the following.  This diagram is generally referred to as the Moody Diagram.




Absolute Roughness is usually defined for a material and can be measured experimentally. Roughness Values are normally given in mm. 

For every circular shape there is diameter and for every non-circular there is Hydraulic Diameter. I personally say it equivalent diameter of a non-circular shape. The hydraulic diameter is not the same as the geometrical diameter in a non-circular duct or pipe. Normally we encounter the two types of non-circular shapes for flow calculations; 1) Rectangular Duct 2) Annular Shape

The hydraulic diameter (aka hydraulic mean diameter) is used for a fluid flowing in a pipe, duct or other conduit of any shape. Hydraulic mean diameter provides a method by which non-circular pipe work and ducting may be treated as circular for the purpose of pressure drop and fluid flow rate calculations. This uses the perimeter and the area of the conduit to provide the diameter of a pipe which has proportions such that conservation of momentum is maintained.

It works well for turbulent flow where geometry is less important, but should not be used for the laminar flow regime, which is influenced to a much higher degree by conduit geometry.

The hydraulic diameter is calculated as 4 times the flow area divided by the wetted perimeter of the conduit. The hydraulic diameter concept applies for rectangular ducts width to height ratio is less than 4 (which is the usual case.

D(h) = 4  x  Area / Wetted Perimeter

where;

D(h) = Hydraulic Diameter
Area = Cross Sectional Area of the Duct
P = Wetted Perimeter of the Duct (Total Length of the surface which is in contact with the fluid in one cross section)


Colebrook-White Equation

For Reynold's Number Greater then 4,000 (Turbulent Flow) the Colebrook Equation is