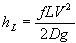Introduction
The Colebrook equation has long been used for calculating the friction factor, f, for in-compressible and some compressible flows in uniform pipes, ducts, and conduits. It is asymptotic to both the accepted smooth-surface and rough-surface pipe equations.
Although widely used, the Colebrook equation is iterative because the unknown friction factor appears on both sides of the equation. To solve for this unknown, one must start by somehow estimating the f value on the right side of the equation, solve for the new f on the left, enter the new value back on the right side, and continue this process until there is a balance on both sides of the equation within an arbitrary difference. (An exact solution to this equation has remained elusive, to date.)
This difference must be small yet accommodate all ε/D (surface roughness/hydraulic diameter) and Re (Reynolds number) values without causing endless computations. The method is labor intensive and complicated even for computers. Add to this the repetitive calculations needed at numerous points in complex flow systems and the task becomes time consuming, to say the least.
For these reasons, many different diagrams have been constructed to simplify the process. A well-known one is the Moody Friction Factor graph. However, reading the chart and interpolating values often leads to inaccuracies. And it would take numerous equations to capture the graphs in software.
A new equation, based on Colebrook’s, has been developed that calculates friction factors in one step.
For ε/D > 0:
This is the Colebrook equation rewritten using a modified Newton iteration for approximating the solution. The modification involves a new factor, A. For ε/D > 0, A is a modified Colebrook equation and calculates the first estimate for the unknown f, or, in this case, 1/f0.5.
Values for f calculated with this equation are based on 69 randomly chosen numbers for Re from 4,000 to 108 and ε/D from 0 (smooth) to 0.05 (rough). They were compared in terms of percent difference from f values calculated with the Colebrook equation after three iterations for each of the same Re and ε/D values (four iterations yielded negligible changes).
For ε/D > 0, all resulting differences are <0.001%. The average difference for all 69 calculations is 0.000134%, with the maximum being 0.000941% and the minimum 0%.
For ε/D = 0, A is derived using leastsquares fit and fine-tuned using trial and error. Only 52 of the 69 numbers were used because of the shorter range of Re (4,000 to 107). All resulting differences are again <0.001%. The average difference for all 52 calculations is 0.000229% with a maximum 0.000519%.
A single equation for A was also developed for all cases:









 = Hydraulic Diameter (m)
= Hydraulic Diameter (m) = Volumetric flow rate (m3/s)
= Volumetric flow rate (m3/s) = Pipe cross-sectional area (m²)
= Pipe cross-sectional area (m²) = Mean Velocity of the Fluid (
= Mean Velocity of the Fluid ( = Dynamic Viscosity of the fluid
= Dynamic Viscosity of the fluid  = Kinematic Viscosity of the fluid
= Kinematic Viscosity of the fluid